Введение в нейросети. Часть 2

1. Кликните по абзацу, который хотите изменить
2. Редактируйте содержимое абзаца, добавляя либо удаляя текст
3. Нажмите на иконку справа, чтобы отправить ваши изменения автору (если вы не зарегистрированы, то увидите сообщение об ошибке)
4. Готово. Теперь нужно лишь подожать, пока автор либо применит ваши изменения, либо откажется от них

Эта и следующие статьи о нейросетях будут не такими простыми для понимания. Базовые знания программирования и школьной алгебры всё же потребуются, потому что я не смогу этот материал объяснить так, чтобы понял и ребёнок, а если и смогу, то это займет слишком много времени.

Бинарная классификация

Мы будем заниматься бинарной классификацией, а именно отличать по изображению кошек от собак. Результатом работы нейросети будет число $y \in \{0, 1\}$, 0 - не кошка, 1 - кошка. 

Для начала нужно преобразовать изображение в такой формат, с которым мы сможем нормально работать. Предположим, что наше изображение 32 на 32 пикселя. Если изображение закодировано в формате RGB, то оно будет состоять из 3 матриц 32x32. Тогда всего пикселей, принимающих значения 0..255 у нас будет 32x32x3 = 3072 пикселей-чисел. Запишем все эти числа в длинный вертикальный список, так называемый вектор. И обозначим его высоту за $n_x$. В нашем случае $n_x$ = 3072:

  $$x = \left[\begin{array}{c}244\\75\\\vdots\\255\\0 \\211\end{array}\right]\text{, }x\in\mathbb{R}^{n_x}$$

Теперь определимся с нотацией.

Единый набор для обучения:

$$ (x, y) \text{ где } x\in\mathbb{R}^{n_x}, y \in {0, 1}$$

$m$ наборов для обучения:

$$(x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), ..., (x^{(m)}, y^{(m)})$$

И определим X как m-набор всех x, то есть список x для всех наборов для обучения. Это будет матрица n x m:

  $$X = \left[\begin{array}{ccc}x_{11}&x_{12}&\cdots&x_{1m}\\x_{21}&x_{22}&\cdots&x_{2m}\\\vdots&\vdots&\ddots&\vdots\\x_{n1}&x_{n2}&\cdots&x_{nm}\end{array}\right]$$

$$ X \in \mathbb{R}^{n_x\times m}$$

То же самое проделаем для Y:

$$Y = [y^{(1)}, y^{(2)}, ..., y^{(m)}]$$

$$ Y \in \mathbb{R}^{1\times m}$$

Логистическая регрессия

Итак, нам на вход будет подаваться изображение в формате $x\in\mathbb{R}^{n_x}$, а результатом будет вероятность того, что на изображении кошка, этот результат мы обозначим $\hat{y} = P(y = 1 \mid x)$

Вот мы и подошли к параметрам нашей нейросети. У нас они будут такими:

$$\omega \in \mathbb{R}^{n_x}, b \in \mathbb{R}$$

То есть $\omega$ - это такой же вектор как $x$, а $b$ - это просто число.

Число $\hat{y}$ (результат работы нейросети) является вероятностью того, что на изображении кошка, и следовательно должно быть в пределах от 0 до 1. Поэтому функция, которую я показывал в первой части, не совсем подойдет, так как её область значений гораздо больше. В таких ситуациях используют сигмоиду - функцию, область значений которой от 0 до 1, она обозначается $\sigma$. Вот её формула:

$$ \sigma(z) = \frac{1}{1 + e^{-z}}$$

График её выглядит так:

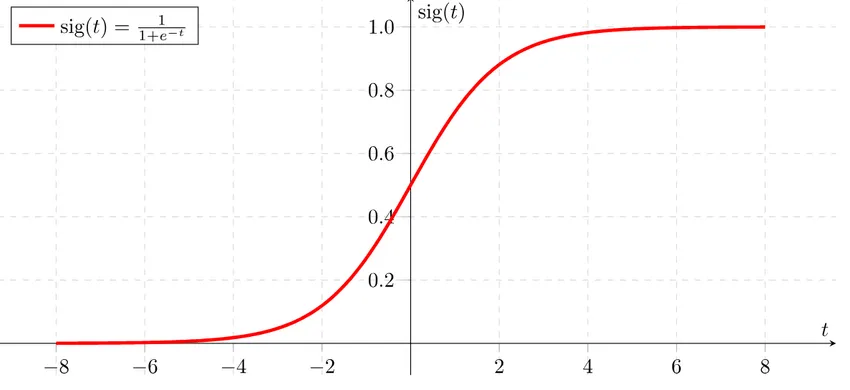
С сигмоидой функция нашей нейросети примет вид:

$$\hat{y} = \sigma(\omega^Tx + b)$$

Мы всё так же перемножаем цифры-пиксели на соответствующие им веса-параметры $\omega$ и добавляем смещение $b$. Только теперь ещё мы всё это обёртываем в сигмоиду, чтобы результат был между 0 и 1.

Символ T в этой формуле означает транспонирование. В общих чертах это просто зеркальное изменение размеров нашей матрицы. Если до транспонирования размеры $\omega$ были 1 x m, то после они станут m x 1. Это необходимо, чтобы правильно выполнить умножение матриц.

Чтобы удобнее было проводить различные вычисления, эту функцию обычно записывают как две:

$$z = \omega^Tx + b$$

$$\hat{y} = \sigma(z)$$

Функция потерь

Нам нужно добиться, чтобы результат работы нейросети $\hat{y}$ был максимально близок к значению $y$ из тренировочного набора:

$$ \hat{y}^{(i)} \approx y^{(i)}$$

$$ i \text{ - номер набора обучения}$$

Для этого нужно понимать, какая сейчас разница межу $\hat{y}$ и $y$. В этом нам поможет функция потерь, которая выглядит так: 

$$ \lambda(\hat{y}, y) = -(y\ln\hat{y} + (1 - y)\ln(1 - \hat{y}))$$

Значение этой функции будет тем меньше, чем меньше разница между $\hat{y}$ и $y$, и тем больше, чем разница между ними больше.

Мы записали функцию потерь для одного тренировочного набора, теперь перепишем её для всех наборов:

$$ \Lambda(\omega, b) = \frac{1}{m}\sum_{i=1}^m \lambda(\hat{y}^{(i)}, y^{(i)}) $$

Теперь у нас всё готово для того, чтобы обучать нейросеть параметрам $\omega$ и $b$. В следующей статье разберём как этого сделать с помощью градиентного спуска.